Resource contributions to system adequacy must be evaluated, both for accurate system adequacy planning and capacity accreditation purposes. Capacity accreditation is used to measure the contribution to system adequacy of individual resources or groups of resources. It is also used in resource procurement and capacity markets. The capacity accreditation process bridges the gap between RA analyses, measuring system risk, and unit procurement, retirement, and capacity market compensation decisions.
Resource contribution is sometimes expressed as a derated capacity, in MW, and sometimes expressed as a percentage of the total capacity. For consistency, all methods outlined in this section use the former approach.
Although resource contribution metrics have historically been calculated on an annual basis, system planners are increasingly considering calculating them on a seasonal basis to account for the intra-annual variability of the RA contributions
Accreditation methods are divided into two main classifications here: probabilistic and approximation methods. Approximation accreditation methods can be further sub-divided into capacity-based and time-period-based methods.
Read more:
Capacity Accreditation: Key Principles, Evolution, and Philosophy. EPRI, Palo Alto, CA: 2024. 3002027010.
Resource Adequacy for a Decarbonized Future: A Summary of Existing and Proposed Resource Adequacy Metrics. EPRI, Palo Alto, CA: 2022. 3002023230.
Modern Resource Adequacy Assessment Methods for Long-Range Electric Power Systems Planning. EPRI, Palo Alto, CA: 2022. 3002025517.
Energy Systems Integration Group. 2023. Ensuring Efficient Reliability: New Design Principles for Capacity Accreditation. A Report of the Redefining Resource Adequacy Task Force. Reston, VA
Probabilistic Accreditation Methods
Probabilistic accreditation methods can be calculated using any probabilistic RA risk metrics. However, they are currently most often calculated using LOLE. The effective load-carrying capability (ELCC) metric is the most notable and at times is erroneously used as an umbrella term for all probabilistic accreditation metrics, but other metrics exist. Other often-used metrics, defined below, are equivalent firm capacity (EFC), and equivalent conventional power (ECP).1
Metric-specific changes to this workflow are noted below. Each example workflow assumes that the reference adequacy metric is in LOLE and that the system starts at the adequacy criteria (e.g., 0.1 days/year). While the system load or supply is often adjusted to meet a certain adequacy target, this is not a necessary step for performing this analysis. This step should be considered with care, as it could have a significant impact on results.
The process for calculating probabilistic accreditation metrics follows a similar pattern across different accreditation metrics:
- A base case system is evaluated to determine the reference adequacy risk metric (e.g., LOLE).
- A change is made to the system (resource addition or substitution), and the metric is remeasured.
- The base case load or supply is adjusted in a certain way until the reference value is restored, and the magnitude of adjustment informs the metric value.
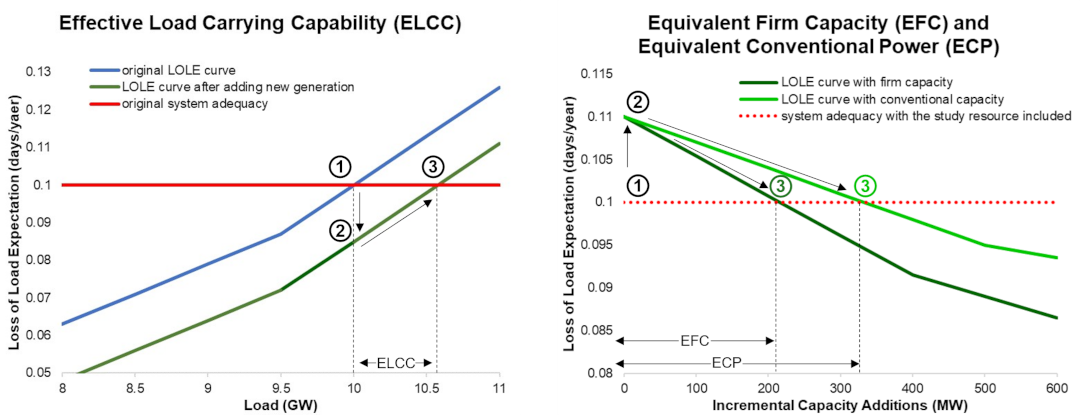
ELCC, EFC, and ECP
Effective Load-Carrying Capability
The effective load-carrying capability (ELCC) of a resource (or group of resources) is defined as the amount by which the system load must increase when a new resource is added to the system to maintain the same system adequacy level.2
The following steps provide an example workflow for determining the ELCC of a generator (as illustrated in the figure above):
- Calculate the starting LOLE of the system. It is found to be 0.1 days/year.
- Add the new generation resource of interest and recalculate the LOLE. It is found to be lower than 0.1 days/year, because adding generation generally improves system adequacy.
- Increase the system load level until the calculated LOLE is equal to 0.1 days/year. The increase in load level required to bring the system back to 0.1 day/year LOLE is the ELCC of the resource.
Following the example of the figure above, at a load of 10 GW, the system is at a LOLE of 0.10 days/year, and when the new generation resource of interest is added, the LOLE decreases. To restore the LOLE to the initial observation, 570 MW of load must be added; this is the resource ELCC. The load addition in step 3 is typically simplified as the addition of a constant load value for every hour of the year, although other methods can be used, which can affect the resultant resource ELCC.
The amount of load added in this exercise is the effective load that can be carried by the new resource at the target reliability level. If, for example a new 100 MW solar resource carries 50 MW of new load before the system returns to the target reliability level, the resource’s ELCC is 50%.
Equivalent Firm Capacity
The equivalent firm capacity (EFC) of a resource (or group of resources) is defined as the amount of firm capacity needed to replace a given resource while maintaining the same system adequacy level. The following steps provide an example workflow for determining the EFC of a generator (as illustrated below):
- Calculate the starting LOLE of the system. It is found to be 0.1 days/year.
- Remove the generation resource of interest and recalculate the LOLE. It is found to be higher than 0.1 days/year, because removing generation generally decreases system adequacy.
- Add a firm capacity resource until the calculated LOLE is equal to 0.1 days/year, within a reasonable tolerance. The size of the final generic generator is the EFC of the resource of interest.
Equivalent Conventional Power
The equivalent conventional power (ECP) of a resource (or group of resources) is defined as the amount of capacity from a conventional dispatchable generating technology (e.g., a combustion turbine) needed to replace the resource while maintaining the same system adequacy level. The procedure for calculating ECP is identical to EFC with one major change: the generation resource added is subject to outages, derates, and other operational limitations. Hence, EFC is sometimes referred to as a special case of ECP. The conventional dispatchable resource assumptions used in the ECP calculation should be documented and communicated when reporting results.
The figure above shows a sample ECP analysis.
Read more:
Additional Considerations for Probabilistic Accreditation
Rather than being static values, ELCC, EFC, and ECP depend on the system in which the corresponding resource is located. A resource’s ELCC, EFC, and ECP are affected by the amount and type of other resources on the system, the underlying load profile, generator outage profiles, and weather conditions, among other factors. All these change over time, thus changing the capacity contribution of a resource, even if it does not change its share of the overall resource mix. Additionally, resources, particularly variable renewable energy and energy-limited resources, interact with one another in either a synergistic or antagonistic manner.1 Also, different orders of resource additions in sequential analyses can yield different results. Evaluating the ELCC of a wind portfolio before solar may result in a different set of ELCC values than evaluating the two resource types in the opposite order. Portfolio considerations when assessing resource capacity value are therefore required. There is potential value in examining these issues from a portfolio-based viewpoint rather than counting capacity contribution of individual resources. However, certain planning and market processes require individual resource accreditation.
Given the interactions between resources, the capacity value of a resource or resource group cannot be calculated when it enters service and never considered again. Instead, the capacity value should be re-evaluated regularly. Additionally, to be as accurate as possible, these metrics should be calculated with many years of data to account for inter-annual variations.
Although evaluating resource contributions using probabilistic methods is more complex and time-consuming than the approximation-based methods described below, results are also more accurate, assuming the underlying system risk assessment is accurate. Additionally, these methods are technology agnostic. While probabilistic methods are often used to calculate capacity accreditation for renewable and storage resources, they can equally be applied to thermal generation.
Interactive Effects between Resources
Resources interact with one another synergistically (their combined capacity contribution is greater than the sum of their parts) or antagonistically (their combined capacity contribution is lesser than the sum of their parts). Following are examples of two types of possible interactions between resources.
Saturation Effect
Adding more capacity of a same resource type to the system (or one with similar characteristics) can lead to a diminishing capacity contribution of that resource type. For wind and solar resources, the output is variable and often correlated with other similar resources in the region. High availability in some periods reduces risk, shifting adequacy risk to periods when output is lower. For energy-limited resources, saturation occurs for two reasons. First, short-duration resources can effectively serve load during system peak conditions, but at higher penetration levels the narrow 3-4-hour peak demand period flattens to wider periods. Second, energy storage resources require resources to charge. Therefore, while storage reduces risk in some periods, it inherently increases risk in others. There may be times when the supply is energy limited rather than capacity limited.
Diversity Effect
This effect occurs when the capacity contribution of a sum of different resources is higher than the sum of its parts. One example of this phenomenon is the pairing of solar and storage resources.2 Just adding solar to the system reduces the duration of the daily peak load and shifts the net peak load to the evening. Additional solar resources added to the system will decrease in capacity value, since risk periods have been shifted to the evening by the first MWs of solar added to the system. Adding only storage to the system can help mitigate peak loads, however, increasing levels of storage duration will be required to flatted load curves after the first MWs are added. Energy storage and solar resources work synergistically when deployed together to achieve greater peak load reduction levels at lower deployed capacities.
Read more:
2 N. Shlag, et al. Resource Adequacy in the Southwest: Public Webinar. E3, 2022
Additional relevant work:
Approximation Methods
Metrics for measuring resource contribution or assigning capacity accreditation can be calculated using several approximation methods. These methods are straightforward to use and explain and can offer a useful approximation for situations in which probabilistic metrics such as ELCC or EFC cannot be calculated because of time constraints or data limitations. Hence, many stakeholders prefer them. However, they are less accurate than probabilistic metrics and should be used only in appropriate situations and be caveated accordingly.
These metrics can be grouped into two broad categories:
-
Capacity-based methods are most often used to assign a capacity value for thermal generators.
-
Time-period-based methods focus only on unit output during high-risk hours and are often used to calculate the capacity value of variable generation.
Capacity-Based Approximation Methods
Installed and unforced capacity are commonly used capacity accreditation metrics used in deterministic approaches for capacity accreditation and to assess resource adequacy through the planning reserve margin approach.
Installed Capacity (ICAP) refers to the nameplate or offered capacity associated with a generating resource.
The Installed Capacity metric is defined as the net dependable rating of a unit. It is typically defined as the summer rated capacity for summer-peaking systems. This metric is sometimes used to quantify the capacity value of thermal units, as it is straightforward to use and understand. However, this metric overestimates the capacity contribution of a unit, as it does not account for forced outages or partial derates.
Unforced capacity (UCAP) derates installed capacity by a factor typically derived from a unit’s forced outage rate (FOR).
The Unforced Capacity metric is typically used to quantify the adequacy contribution of thermal generators. It is defined as the amount of physical generating capacity available after accounting for a unit’s forced outage rate.
This metric is likely less accurate than probabilistic metrics. However, it is straightforward to calculate and provides a reasonable approximation of adequacy contribution for thermal resources in a large electricity system with many generators, assuming outages are uncorrelated.1 Furthermore, thermal resources in large systems do not typically exhibit interactive effects, unlike variable and energy-limited resources. However, large generator outages could have an outsized impact on adequacy in a small system if they occur during a peak demand period. Hence, the UCAP metric is typically only applied to thermal resources in large systems and assumes no underlying common cause of outages.
Read More:
Time-Period-Based Methods
Time Period Selection
The first step to calculating capacity value using Time-Period-based methods is to define the relevant time period considered. This is specific to the system studied and should be thoughtfully evaluated.
Peak load periods are typically used as a proxy for the most at-risk time periods of a system. This method works best in systems with a high correlation between periods of peak demand and maximum system risk. As system risk shifts away from periods of peak demand, as is seen increasingly in systems with high renewable penetration, this metric becomes less accurate. High renewable-penetration systems should instead consider defining the capacity value of the resource as its available generation during peak net load.
Summary Statistic Selection
Several summary statistics can be used to aggregate the available energy of the resource over the time period selected.
Most commonly, the capacity value of a resource is defined as the mean output of its available generation during the defined time period. This method is straightforward to calculate and understand and is easy to explain in regulatory and other public proceedings. When the relevant time period is defined as the peak LOLP hours, an alternative to this method defines the capacity value of a resource as its available generation during peak LOLP hours normalized by the LOLPs of the system. Hence, this technique places higher weight on resource contribution during periods of RA deficiency.
Alternatively, the capacity value of a resource can be defined using the exceedance method, which is sometimes referred to as the percentile method. This method defines the capacity value of a resource as the minimum available energy output produced by this resource during selected at-risk hours. For example, suppose the exceedance level is defined as 70%. In that case, the capacity value assigned to the resource is the generation amount that it is available to produce at least 70% of the time during the defined at-risk time period. Planners sometimes use this method when seeking to adopt a conservative approach to variable resource capacity valuation. However, this method understates the capacity contribution of a resource, as all available generation below the exceedance level is excluded from the calculation. Moreover, this method does not capture the full distribution of available generation above the exceedance level. A plant with available energy production in excess of its exceedance level for most of the relevant time period is assigned the same capacity value as a plant with much lower average available generation. A potential workaround is to use the CVaR metric, described below, which measures the average outcome of all generation above the exceedance level.
VaR and CVaR
VaR (Value at Risk) is a probabilistic metric used to assess risk. It represents the maximum expected loss over a specified time period under normal market conditions, at a given confidence level. In the context of resource accreditation, VaR helps estimate the potential shortfall in a resource’s capacity contribution. For example, if a resource has a VaR of 100 MW at a 95% confidence level, there’s a 5% chance that its capacity contribution will fall below 100 MW.
CVaR (Conditional Value at Risk) goes beyond VaR It provides an average of the losses that exceed the VaR threshold. In other words, CVaR considers the tail risk—the extent of potential losses in scenarios where actual losses surpass the VaR. Calculating CVaR involves integrating the tail of the loss distribution. For resource planning, understanding both VaR and CVaR helps quantify risks associated with resource contributions and ensures the reliability of the electric power system.
